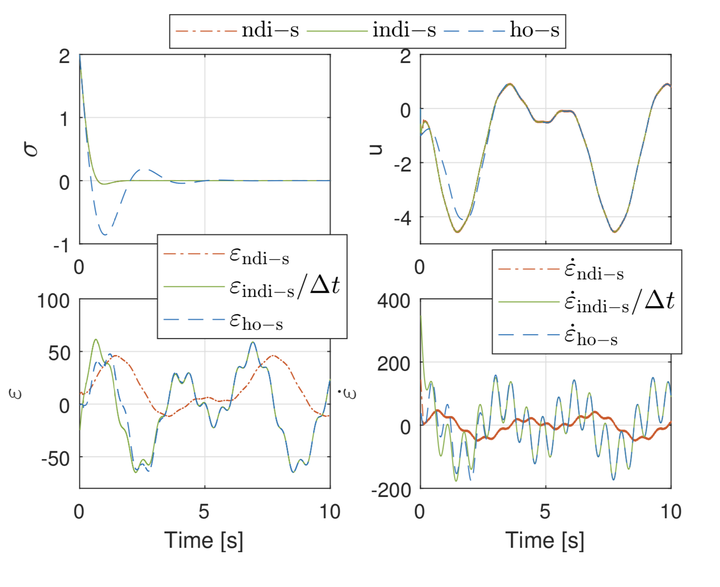
 A simulation comparison case.
A simulation comparison case.
Abstract
For mitigating the chattering effect in the sliding mode control (SMC), many adaption mechanisms have been proposed to reduce the switching gains. However, less attention is paid to the control structure, which influences the resulting uncertainty term and determines the minimum possible gains. This paper compares three control structures for inducing higher-order sliding modes in finite time, i.e., nonlinear dynamic inversion (NDI) based SMC, higher-order sliding mode control (HOSMC) with artificially increased relative degree, and the recently proposed incremental nonlinear dynamic inversion (INDI) based SMC. The latter two control structures have reduced model dependency as compared to NDI-SMC. Moreover, their nominal control increments are found to be approximately equivalent if the sampling interval is sufficiently small and if their gains satisfy certain conditions. Under the same circumstances, the norm value of the resulting uncertainty using INDI-SMC is several orders of magnitude smaller than those using other control structures. For maintaining the sliding modes, the minimum possible gains required by HOSMC approximately equal those needed by INDI-SMC divided by the sampling interval. Nevertheless, these two approaches have comparable chattering degrees, which are effectively reduced as compared to NDI-SMC. The analytical results are verified by numerical simulations.