Nonlinear Control Theory
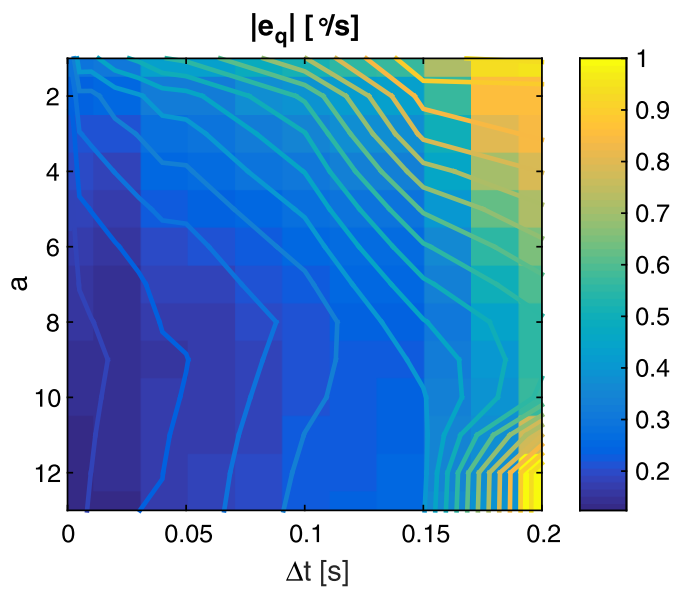 Influences of sampling interval and gains on the ultimate bounds.
Influences of sampling interval and gains on the ultimate bounds.
This page contains our contributions to the control community. We proposed a new sensor-based incremental control framework for generic multi-input and multi-output nonlinear systems with an arbitrary relative degree. The closed-loop stability in the presence of model uncertainties and external disturbances are proved using Lyapunov methods. The robustness of the system to regular and singular perturbations are also analyzed.
For mitigating the chattering effect in the sliding mode control (SMC), many adaptation mechanisms have been proposed to reduce the switching gains. However, less attention is paid to the control structure, which influences the resulting uncertainty term and determines the minimum possible gains. Our research compares three control structures for inducing higher-order sliding modes in finite time: nonlinear dynamic inversion (NDI) based SMC, higher-order sliding mode control (HOSMC) with artificially increased relative degree, and the recently proposed incremental nonlinear dynamic inversion (INDI) based SMC.
We also define the controllability margin (CM) and observability margin (OM) from the view of singular perturbation and regular perturbation. The model error structure (MES) is proposed as a structural property metric for linear systems based on the novel concepts of singular perturbation margin (SPM) and generalized gain margin (GGM).